惯性微流控计算方法的最新进展与未来展望，机器学习有潜力带来变革
2025-11-02 10:53:50   来源：麦姆斯咨询   评论：0   点击：

惯性微流控是一种通过流体惯性在微流道中实现细胞定位来操控细胞的有效方法。该方法广泛应用于流式细胞术、液体活检、血液分离和细胞分选等领域。迄今，已有大量研究广泛探索了惯性聚焦的原理和涉及的流体动力学，特别是作用于颗粒的升力。现在普遍认为，惯性聚焦通常是壁面诱导力和剪切梯度力之间平衡的结果。通道曲率或非牛顿流体介质的添加可以调节这种力平衡，改变平衡的横截面位置。

对惯性聚焦和粘弹性聚焦的理解在很大程度上是通过简化模型发展起来的。然而，当前的实验技术在研究更复杂的通道几何形状、可变形颗粒，或需要结合惯性和粘弹性效应的场景时，在特定精度水平方面存在局限。随着使用这些组合效应以及复杂器件的应用日益普遍，越来越需要提高对控制非牛顿流体、非球形可变形颗粒以及曲面通道微流控系统中惯性迁移动力学基本原理的理解。

从历史发展来看，有限元法（FEM）和格子玻尔兹曼法（LBM）等数值模型一直被用于探索微流控系统的基本物理原理。这些技术在求解速度场、压力场以及研究颗粒-流体相互作用方面发挥了关键作用，其结果通常通过实验数据进行验证。然而，随着微流控系统发展到包含更复杂的通道几何形状，并应用于更复杂的生物样品，标准的数值技术已不足以应对增加的复杂性，因此，需要新的计算方法来有效解决这些挑战。

据麦姆斯咨询介绍，美国伊利诺伊大学芝加哥分校的研究人员近期在Microsystems & Nanoengineering上发表了一篇题为“Computational methods for inertial microfluidics: recent advances and future perspectives”的综述性文章。该综述旨在概述现有的各类数值技术，并重点阐述其优缺点。研究人员探讨了计算惯性微流控的最新进展，重点介绍了过去四年来的发展，以及平滑粒子流体动力学（SPH）等创新方法的兴起。此外，文章还介绍了机器学习在惯性微流控领域的应用价值，指出其应用仍相对有限，强调了其变革潜力，同时也指出了其发展过程中亟待克服的挑战。

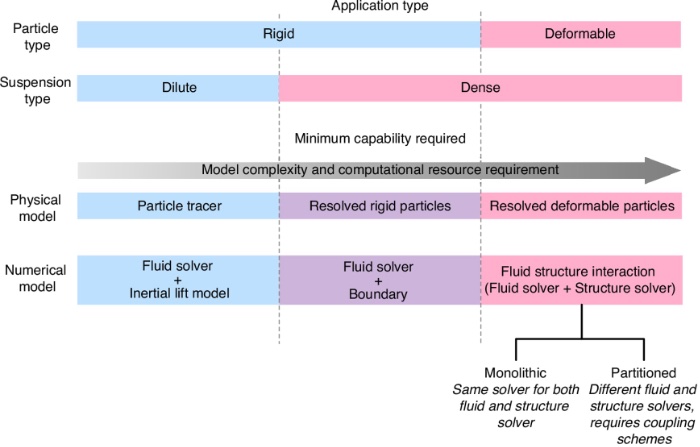
最小建模要求

模拟惯性微流控器件数值方法的选择，主要取决于具体应用，以及精确表征相关机制所需物理模型的复杂性。通常，随着物理模型复杂性的增加（即包含更多物理现象），数值模型的复杂性和所需的计算资源也会增加。目前，已有多种数值方法被广泛应用于惯性微流控模型的研究，包括FEM、LBM和SPH等。该综述分别详细介绍了相关进展。

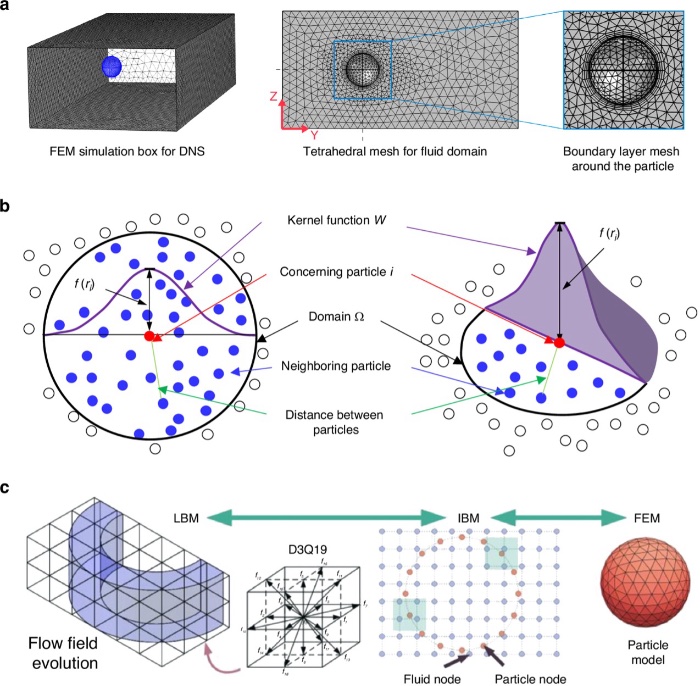
流体流动和流固相互作用的主要数值方法和耦合策略

近年的相关研究进展有限，特别是在处理非牛顿流体的非线性现象以及非球形可变形颗粒方面。为有效推动该领域发展，包括剪切流中的自对准、自定向或旋转稳定性等问题，亟需借助高性能计算和现代模拟方法。该综述用表格总结了文中讨论的常用数值方法。这些先进工具有望为惯性微流控研究开辟新方向，为突破性发现奠定基础。

惯性微流控中基于模型复杂度的常用数值方法

基于网格的数值方法（例如FEM）在分析惯性升力以及优化微流控器件设计方面发挥了关键作用。这些方法在具有明确流体流动和相对简单几何形状的场景中特别有效。然而，当处理复杂流体动力学问题时（包括自由表面、可变形边界、移动界面、大变形和流固相互作用等），它们会面临局限性。在这种情况下，LBM结合浸入边界法（IBM）已成为一种有效解决方案，以克服传统方法的局限性。这种技术提供了灵活性、精度和计算效率，使其适合捕捉微通道中的流固相互作用。将这些方法与传统方法相结合，可以发挥互补优势，并进一步减轻各自的局限性。然而，耦合算法的选择和实现可能具有挑战性，并且可能因具体应用而异。使用IBM和LBM方法，特别是与FEM结合使用时，可能会涉及更高的计算成本，因为它们对于特定问题可能比传统FEM要求更高。因此，选择最合适的数值方法，取决于问题的性质和可用的计算资源。

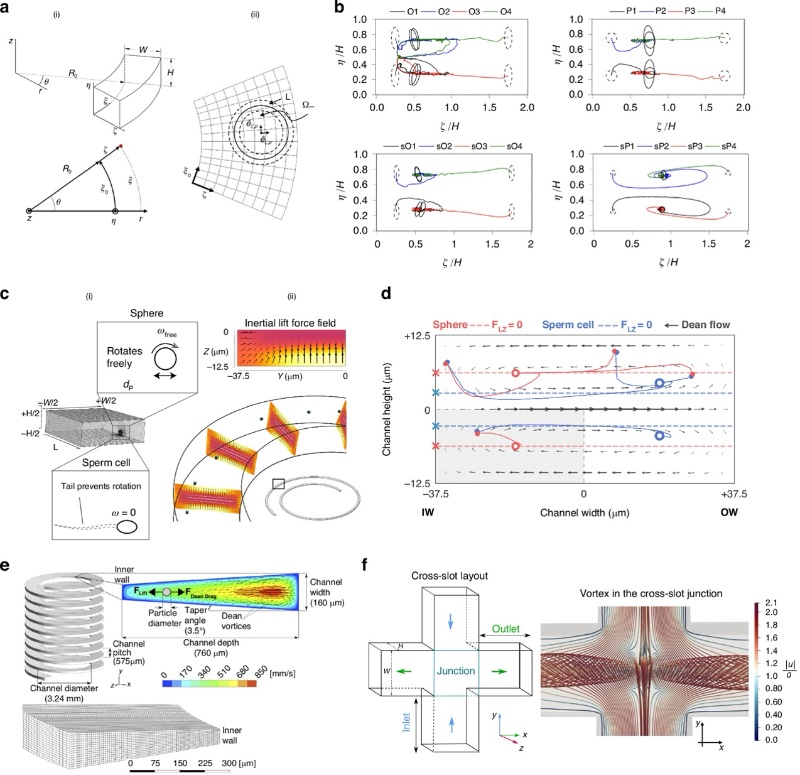
非直通道微流控器件的建模策略和结果

近年来，SPH等无网格粒子方法在流体力学领域得到了广泛应用。SPH因其能够处理复杂变形并保持优异的守恒特性，被广泛用于模拟流固力学。SPH非常适合模拟复杂微流控环境中的颗粒行为。该方法已被用于分析球形和椭球形颗粒在惯性力作用下在微通道中的迁移和旋转。SPH模拟结果已通过数值模拟、解析解和实验观测结果进行了验证，确立了SPH作为模拟惯性微流控中颗粒行为的一种重要替代方法。

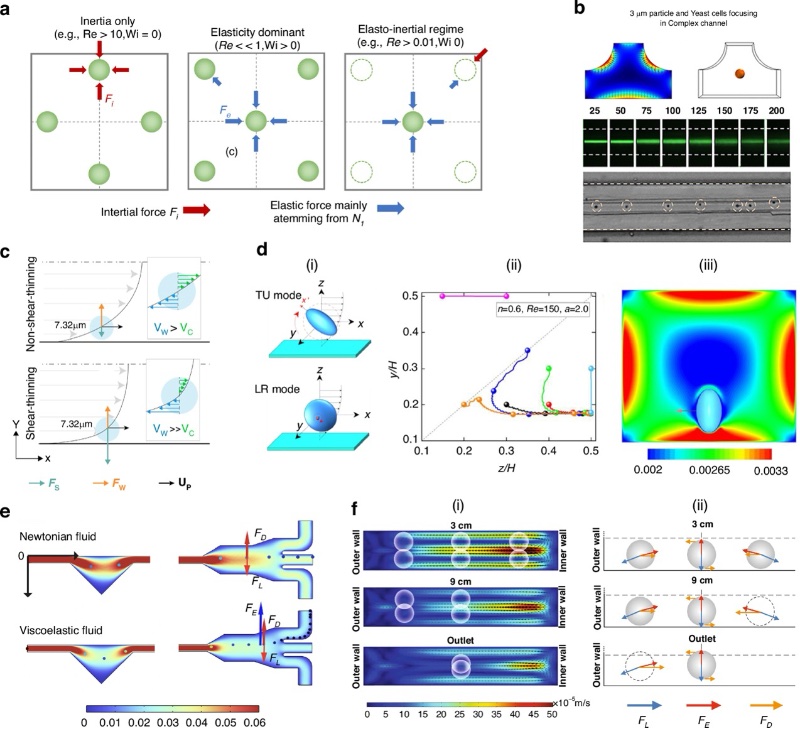
弹性惯性聚焦机制和模拟非牛顿流体中颗粒迁移的最新进展

将机器学习技术与惯性微流控相结合，在变革微流控器件的设计和运行方式方面展示了显著潜力。这种结合包含几个关键方面。首先，机器学习可以简化数据处理并压缩任务，允许对复杂微通道几何形状中的颗粒行为进行预测建模。与实验数据相比，其能够高效管理从数值模拟中产生的大规模数据集，这一点尤具优势。机器学习还可以作为数值模拟与实验数据之间的互补桥梁，增强预测的总体普适性。其次，机器学习技术展示了在存在偏差的数据上有效泛化并适应其固有的高方差特性。这在与相对精确的数值模拟相结合时，特别有助于降低实验数据产生的误差。鉴于惯性微流控在微观尺度上运行，即使微小误差也可能导致与预期结果出现显著偏差，因此机器学习算法能够利用微流控数据构建稳健模型的能力至关重要。第三，当前的研究工作主要集中在开发适用于惯性微流控独特需求的机器学习技术。持续的研究对于识别该领域的建模需求，并深入探索机器学习数学的广阔领域以寻找合适的解决方案至关重要。这种探索旨在创建能够精确预测各种微流控系统中颗粒动力学的机器学习模型，特别是在这些系统变得越来越复杂的背景下。

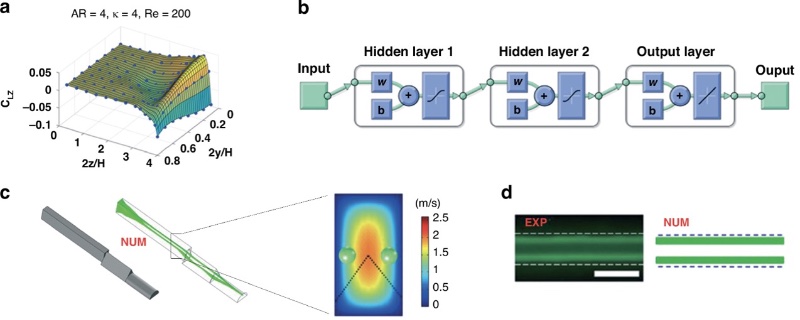
机器学习辅助预测颗粒惯性聚焦

将机器学习与惯性微流控融合的总体目标是实现自动化，涵盖从设计阶段到控制和操作的全流程。这需要开发能够预测各种应用中颗粒惯性动力学的机器学习模型，包括颗粒分选、分离和聚焦等。这种自动化有潜力显著加速最先进微流控器件的研发进程。为了充分实现这一潜力，未来的研究应深入探索考量粘弹性流体、颗粒形状和可变形性等额外因素的复杂系统。对于弹性流体，引入威森伯格数（Wi）等参数，可以提供对流体特性的更精细控制。随着微流控应用变得更加复杂，可能需要采用具有更多隐藏层的深度神经网络，特别是随着数据集的扩展和变量的积累，当然，有效管理随之而来的计算复杂性同样至关重要。

论文链接：https://doi.org/10.1038/s41378-025-00992-6

延伸阅读：

《微流控技术及市场-2024版》